只有神才能写出的代码 – 唐玥璨

神也是人,只不过他做到了人做不到的事——阿木

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y;    // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );               // what the fuck? 
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
    // y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

    return y;
}

上面这段代码不知道是否有人知道？在这段代码之中的最为人津津乐道的是这一句：i = 0x5f3759df - ( i >> 1 ); // what the fuck? 包括里面的注释那句经典的what the fuck? 足以发现写出这段代码的人自己也不知道为什么，特别是这个魔法值：0x5f3759df ，简直莫名其妙对吧。

然而这段代码是这个世界上三维引擎的起源，任何一个具备三维渲染能力的程序的诞生都要好好的感谢的这段代码和无偿将其开源的公司id software，和那位我心目中的神，传奇程序员——约翰·卡马克。

第一章：什么叫做性能优化？

首先上面这段代码可以从函数名称就看出他是干嘛的，简单来说就是求一个浮点数的平方根倒数公示就非常简单：

\(y=\frac{1}{\sqrt{x}}\)

对X开根号运算，最后再求倒数，简单的不能再简单了，但是各位可以试想一下，对于计算机而言，直接运行这个公式计算量是比较大的，就因为里面存在的√x，对于32位二进制表示的浮点数进行乘法或者除法运算对应的运算量就已经很夸张了，对于这个开方运算而言传统CPU运算它效率可想而知是多么的低。你可能会问你写什么程序需要用这个公式呀，这不是吃饱了撑的吗？诶，还真不是，这是人类历史上第一个具备动态光源的三维游戏：《雷神之锤III》里面的代码（这个游戏被其开发公司开源了，你可以在这里找到）。

各位三维游戏之中的动态光源是一个非常重要的设计，有了光源的存在可以照亮游戏之中的三维场景，在1999年，全世界第一次见到拥有动态光影的游戏时间是多么魔幻的一个事。各位要知道那个时候的游戏还是任天堂FC的时代，三维游戏本身的数量就及其的稀少，而动态光源渲染几乎可以说是一件不可能的事情，最要的原因便是计算的效率，这也和我们上文提到的公式有关。再进一步讨论之前有必要解释一下动态光源是如何计算的。

上面这个图是我从WebGL原理说明的一个网站上拔来的（网站地址）这个文章已经说的非常简单了，你可以试着拖动rotation条看看在点光源的情况下，绘制表面的颜色应该计算，其实在这个图的加持下已经非常清晰了，答案就是用平面上任意点的法向量点乘这个点与光源的方向向量，我也像模像样搞个公式放下面：

\(光照强度=点在平面的单位法向量·光源与点连线的向量\)

那么谁还记得向量的点乘公式？当然点乘不是什么重点，在这个计算之中光源与点连续的向量很简单，就是浮点加法而已，但是这个平面的单位法向量就要了命了，例如在空间直角坐标系中平面\(Ax+By+Cz+D=0\)的法向量为\(n=(A,B,C)\)，而它的单位法向量即法向量除以法向量的长度，正负代表方向。

\(±\frac{(A,B,C)}{\sqrt{A^2+B^2+C^2}}\)

这个公式就很简单了，各位这不就是平方根倒数吗？所以当年为什么雷神之锤III可以一鸣惊人，但是没有人见过动态光源居然可以实时运算，同时对于游戏而已，光源在运动，当年的游戏哪怕全屏只有十万个多边形，每一个多边形的每一个像素都需要计算法向量，同时游戏起码需要每秒计算超过45次吧也就是达到45FPS以上，这样玩起来才会流畅，所以各位当年的计算机甚至没有独立的图形卡，这个游戏几乎是纯CPU计算，想要做到上述性能要求几乎可以说每秒需要执行超过上百万次的平方根倒数运行，现在大家应该可以理解这个平方根倒数是一个多么庞大的性能开销了吧？如果不对开方运算进行简化，当年的游戏是绝不可能实现动态光照计算的。

上述的所有的铺垫只是为了解释清楚什么才叫做游戏的性能优化，真正意义上能够和同行拉开差距的优化都是在数学层面下功夫，你减少阴影距离，我降低贴图分辨率这些只能说是无可奈何的低能优化，上述基本的优化才是核心技术！

第二章：魔法值0x5f3759df的来历

首先各位是否知道计算机是如何计算\(\sqrt{x}\)的吗？这种运算首先就不可能是直接计算，而是采用类似夹逼法迭代来的，没错你要是手算也只有这个办法，这得感谢老祖宗牛顿，真正的巨人，这个方法叫做牛顿迭代法，公式如下：

\(x_{n+1}= x_n -\frac{ f(x_n)}{f'(x_n)}\)

其中\(x_n\)表述迭代的结果值，n表示迭代的次数，假设求\(\sqrt{5}\)，我们设置第零次迭代的初始\(x_0=2\)，那么带入公式可得\(f(x)=x^2-5\)

第一次迭代：

\(x_1= 2 -\frac{2^2-5}{2\times2}=2.25\)

第二次迭代：

\(x_2= 2.25 -\frac{2.25^2-5}{2\times2.25}\approx2.236111111111111\)

第三次迭代：

\(x_3= 2.236111111111111 -\frac{2.236111111111111^2-5}{2\times2.236111111111111}\approx2.236067977915804\)

其实迭代到第二次就一个可以获取一个足够精确的值了，但是问题在于对于5而言我们找平方根可以猜测为2，但是任意数据\(x\)的平方根怎么猜测初始值呀？这就要看神奇的二进制如何发挥功效了，我们来拆解一下i = 0x5f3759df - ( i >> 1 )，首先我们带入原始的公式可以得到：

\(y=\frac{1}{\sqrt{x}}=x^{\frac{1}{2}}\)

进而可得：

\(log_2(y)=-\frac{1}{2}log_2x\)

我们可以认为y、x都是浮点数，带入浮点表达式可得：

\(log_2(2^{(E_y-127)}\times(1.0+\frac{M_y}{2^{23}}))=-\frac{1}{2}log_2(2^{(E_x-127)}\times(1.0+\frac{M_x}{2^{23}}))\)

做一下简单的变化：

\((E_y-127) + log_2(1.0+\frac{M_y}{2^{23}})=-\frac{1}{2}(E_x-127)log_2(1.0+\frac{M_x}{2^{23}})\)

看到这里我知道大家都懵了估计，肯定有人会问这个\(2^{(E_y-127)}\times(1.0+\frac{M_y}{2^{23}})\)是个什么东西，从哪里冒出来的。不要急，这个东西需要结合浮点数才能解释清楚，大家肯定都知道所谓浮点数其实是32个字节表示的小数，一堆0和1是怎么表示小数的？其实非常简单，甚至过于简单了，极其符合直觉。试想一下小数天然可以使用科学记数法表示，我们拿0.15625为例，具体如下：

\(0.15625=1.5625 × 10^-1\)

然后我们进行分析一下，12.5用科学技术法可以分为三个部分，首先他是正数，所有需要一个东西记录数值的±值，然后\(1.5625 × 10^-1\)可以分为数值部分1.5625和指数部分-1，这其实就是浮点数的定义（IEEE 754标准）：

符号位（1位）：表示数值的符号，0表示正数，1表示负数。
指数位（8位）：表示幂的值。这8位被分为两部分：前3位表示指数的偏移量（bias），后5位表示指数的实际值。
小数位（23位）：表示小数部分的数值。这23位被分为两部分：前1位是尾数（Mantissa）的符号位，后22位是尾数的值。

所以对应规范，第1位bit是正负号；8个bits（1个byte）是幂 (Exponent，后面记为E)；后23个bits是小数位 (Mantissa, 后面记为M)我们就可以得到浮点数y的二进制整数表达：\(2^{(E_y-127)}\times(1.0+\frac{M_y}{2^{23}})\)。然后我们接着做推理。你肯定回想，这个\((E_y-127) + log_2(1.0+\frac{M_y}{2^{23}})=-\frac{1}{2}(E_x-127)log_2(1.0+\frac{M_x}{2^{23}})\)式子看着就不简单怎么最后会得到一个常量，不要急，我们做一下简单的简化，首先来一个小小的震撼，或者或来一个暴论：

\(log_2(1+x)\approx x+0.045(0<x<1)\)

为啥这么说呢？请看下图：

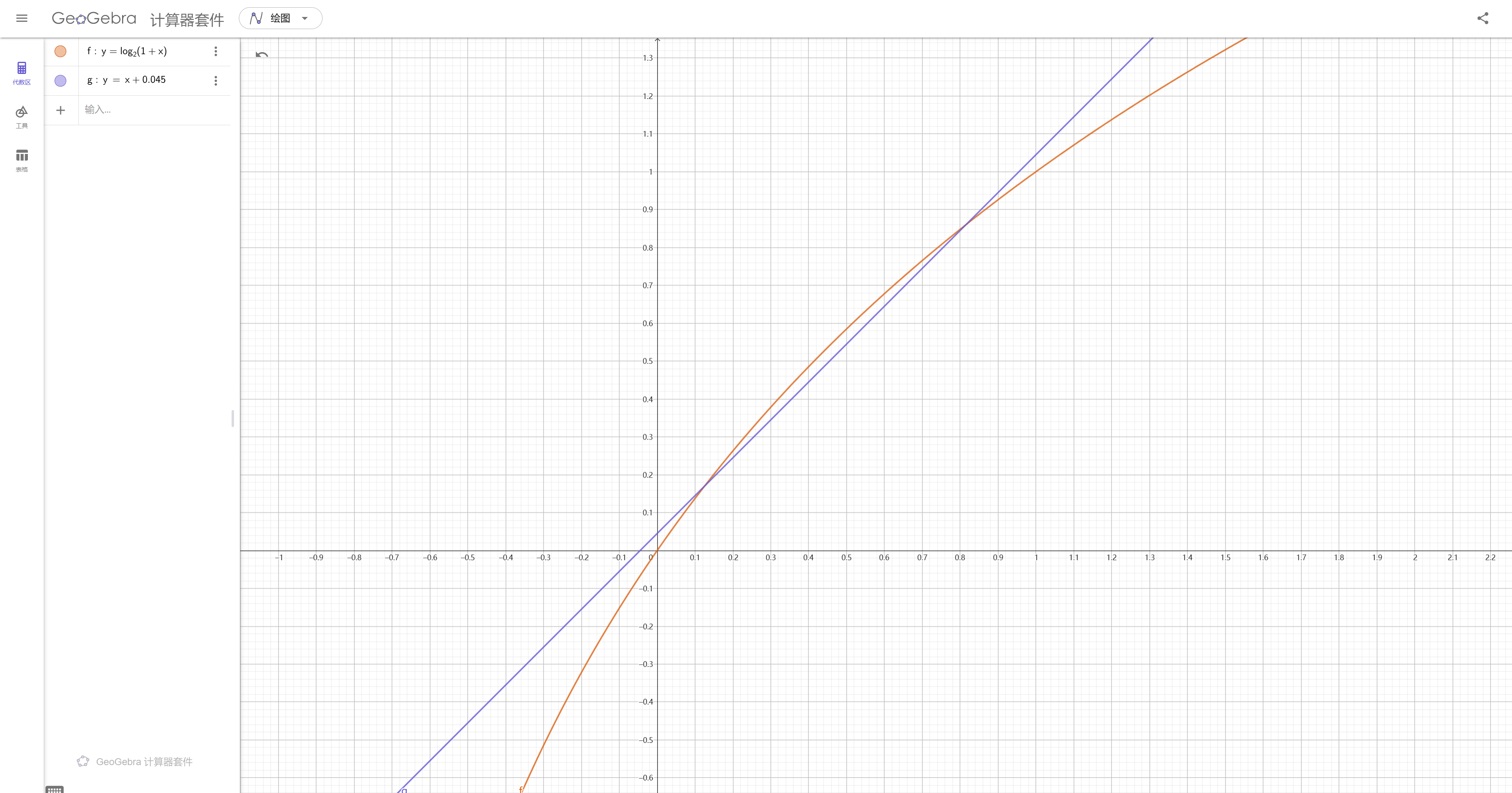
可以发现在我们本来就是为牛顿迭代找一个足够精确的初始值，那么一个近似的同时又足够简单的计算才是我们需要的，所以把\(k=0.045\)带入到算数式之后简化可得：

\((E_y – 127) +\frac{M_y}{2^{23}} + k = -\frac{1}{2}(E_x – 127) – \frac{1}{2}(\frac{M_x}{2^{23}} + k)\)

进一步简化之后可以得到：

\(2^{23}E_y + M_y = \frac{3}{2}(127 – k)2^{23} – \frac{1}{2}(2^{23}E_x + M_x)\)

接下来就是见证奇迹的时候，我们知道浮点数\(y\)的二进制表达之后假设把浮点数强行转为整数会发生什么？没错整形状态下的\(y\)就是\(2^{23}E_y + M_y\)，同时对于整形二进制而言除以2就等于是将二进制数右移，所以最终的表述方式则为：

\(i = \frac{3}{2}(127 – k)2^{23} – (i >> 1)\)

同时，这个式子里面的常量\(\frac{3}{2}(127 – 0.045)2^{23}\)想象聪明的你已经知道了：

\(\frac{3}{2}(127 – 0.045)2^{23} \approx 1597463007\)= 0x5f3759df(转16进制)

所以最后我们再来看看这段代码：

i = * ( long * ) &y; // 浮点数强行转为整形
i = 0x5f3759df - ( i >> 1 ); // 计算牛顿迭代的初始值
y = * ( float * ) &i; //将初始值结果转为浮点数
y = y * ( threehalfs - ( x2 * y * y ) ); // 平淡无奇的第一次牛顿迭代

现在，你是不是发现这四行代码简直就是优雅的极致！！！

第三章：真正的历史

我的偶像虽然是约翰卡马克，但是说实话这个代码不是他写的，而是拿来主义抄过来的，他当时自己也不知道为啥这玩意可以计算平方根，所以才留下了那个闻名世界的what the fuck?

那么到底是那个天才写出来的呢？下面的内容就没有那么的严谨了，主要是历史资料可靠性已经不是那么的完整了，一般来说认为实际找到这个0x5f3759df魔法值的人叫做克雷格沃什（我甚至连照片都找不到了），这个老哥当年在一家超算公司上班，公司要求他在当时的垃圾电脑上实现三维绘图功能（类似MATLAB），这个老哥没有办法可以说是闭关搞出了这个算法，然后这家公司的内部其他程序员跳槽到3dfx，最后3dfx的另一个程序员跳槽到id software之后，这个代码才流转到约翰卡马克的手里。

这个算法的历史意义是什么呢？这么说吧，现代CPU/GPU芯片内部的处理器集成的指令集就包括了这个算法，我们在现代程序员开发代码只需要调用math.h硬件层面就自动完成了上面这个完美代码的运行，节约了大家多少头发呀。最牛逼的在于约翰卡马克在游戏上市之后就将游戏的源代码直接开源了，这样大家才认识到这个算法。

可悲的事情是什么？做出这么大共享的人，没有获得图灵奖，甚至我都找不到他的照片！

第四章：总结

我们天天上班当打工人，每天处理的问题都是一些业务代码，NB一点的程序员搞搞框架代码、中间件代码，设计一些复杂的业务系统。不少人甚至魔怔了，写个破前端或者后端混到小组leader就觉得自己NB了，可以了。后端天天吹的是什么上万并发如何处理、海量数据怎么查询，前端开发在网络上天天撕逼什么react和vue哪个好用，各位，我说个不好听的，你真的不重要！

像我这种前端、后端、桌面端都在写，从业这么多年写了不知道多少万行代码了，看到这个算法还是觉得非常羞愧。我当年看着柏林噪声函数区区一百行代码头皮发麻，搞了上上下下一个月才算弄明白。现在呢，是个前端就敢往简历上写WebGL，结果面试一问，甚至连向量的点乘和叉乘都不知道，还大言不惭的说WebGL是多出来东西，就这？这也太浮夸了吧？我认为做技术的人就应该做技术，别说什么技术合伙人被踢出局，技术不值钱，技术不能吃一辈子，各位扪心自问，你的现在学会的技术真的值钱吗？在我看来很多程序员连门都没有入的情况下就非要去做什么项目经理、产品经理，想要转管理岗。好家伙，我想反问一句，你凭什么觉得项目经理、产品经理、技术管理是个简单的活？

《只有神才能写出的代码》有4条留言

留下回复取消回复